周期駆動系で量子情報の非局在化を実証

－学術研究のための量子コンピュータの本格利用が開始－

クオンティニュアム

2025年4月11日 14時00分

2025年4月11日

理化学研究所

クオンティニュアム株式会社

慶應義塾大学

※本プレスリリースは3者による共同名義のプレスリリースのため、重複して届く可能性がございます。ご了承ください。

概要
　理化学研究所（理研）量子コンピュータ研究センター量子計算科学研究チームの関和弘研究員、開拓研究所柚木計算物性物理研究室の柚木清司主任研究員（計算科学研究センター量子系物質科学研究チームチームプリンシパル、量子コンピュータ研究センター量子計算科学研究チームチームディレクター、創発物性科学研究センター計算量子物性研究チームチームディレクター）、クオンティニュアム株式会社の菊池勇太リードR&Dサイエンティスト（理研数理創造研究センター客員研究員）、慶應義塾大学医学部の早田智也准教授（理研数理創造研究センター客員研究員）の共同研究グループは、周期駆動系を模した量子回路[1]を用いることで量子情報が非局在化した状態（スクランブリング状態）を準備できることを、イオントラップ型量子コンピュータ[2]を用いて実証しました。

　スクランブリング状態は、量子情報の復元や量子多体系[3]計算に役立つことが期待される性質を持っています。本成果は、物理現象と量子情報が交錯する学術研究領域における黎明（れいめい）期の量子コンピュータ利用事例として、日本における量子コンピュータ利用の促進に貢献すると期待されます。

　今回、共同研究グループは、これまでランダム性を持つ量子回路[1]を用いて議論されることが一般的だったスクランブリング状態を、周期駆動系を模した量子回路を用いても準備できることを、高い忠実度で量子操作が可能な量子コンピュータの実機を用いて、適切なエラー緩和法と理論的考察の組み合わせにより確かめました。

　本研究は、科学雑誌『Physical Review Research』オンライン版（4月10日付）に掲載されました。

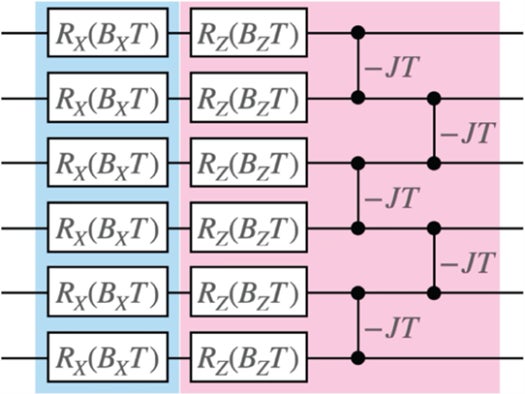
背景
　量子力学に従う物理系を巧みに用意し、制御し、情報を得る手段は、長年にわたって発展を続けています。その発展の中で、近年注目を集めているのが量子コンピュータです。量子コンピュータでは、物理系の構成要素である量子ビット[4]群に対し、量子力学的な操作を施すことでその状態を変化させ、量子ビット群をある状態に準備し、測定を行うことで情報を取得します。

　特に、従来のコンピュータでは表現が難しい状態を準備し、それに対して適切な測定を行うことで、従来のコンピュータでは処理すべきデータが爆発的に増えて計算が困難な課題を、計算にかかる時間やエネルギーなどの指標においてより効率的に解決することが、量子コンピュータに期待されています。

　現時点で利用可能な量子コンピュータは、計算途中で生じた誤りを訂正しながら計算を進める誤り耐性量子コンピュータではなく、それと区別してNISQ[5]（ノイズあり中規模量子コンピュータ）と呼ばれています。NISQでは、時間経過や量子力学的な操作に伴い、意図しない状態変化（誤り）が蓄積します。その結果、以下のような難しさが生じます。（1）実行できる量子力学的な操作数に事実上の制限があること、（2）得られる結果は誤りがないと仮定した場合に期待される結果とは一般に異なることです。このような難しさに対処しつつNISQ上で課題の遂行に役立つと期待される状態を実際に準備することは、短期的にはNISQを利用した研究開発の促進につながり、長期的には誤り耐性量子コンピュータが実現した後に、これを活用するためのアルゴリズム開発の進展に寄与すると考えられます。

　今回、共同研究グループは、イオントラップ型量子コンピュータを用いて、量子情報が非局在化した状態（スクランブリング状態）を準備することに取り組みました。この状態は、量子情報の復元や量子多体系計算に有用な特性を持ち、さまざまな量子アルゴリズムの一部として利用できることが期待されます。

研究手法と成果
　共同研究グループは、外界から孤立した物理系が周期的な駆動を受けて加熱される現象を模した量子回路（周期駆動系の量子回路）を、クオンティニュアム社の二つのイオントラップ型量子コンピュータである「H1-1」と「H1-2[6]」に実装することで、スクランブリング状態を準備しました。

　本研究ではまず、スクランブリング状態が生成できているかどうかを検証しました。加熱現象との類推から、周期駆動系の量子回路で生成した状態の部分系に着目すると、駆動の回数が十分に大きいときは、高温の（ランダムな）状態と区別がほとんどつかないと予想されます。一方で部分系のみに着目するとランダムな状態に見えるという状況から、系全体としては量子情報が非局在化した状態、つまりスクランブリング状態になっていることが示唆されます。ただし、量子回路自体から加熱現象を記述するためのエネルギーや温度などを唯一に定義することはできません。そこで、生成した状態がスクランブリング状態にあってしかるべき性質を持つことを、エネルギーや温度の概念を用いずに、量子情報理論[7]の観点から検証しました。

　検証には以下の二つの方法を用いました。まず、周期駆動系の量子回路の一部分に投入した量子状態の復元を試みたときの成功確率と忠実度の計算[8]を行いました。さらに、この周期駆動系の量子回路によって引き起こされる量子情報の非局在化の指標を計算[9]しました。

　まず、量子コンピュータ実機のノイズがこれら二つの計算結果に与える影響を評価するため、ノイズモデルを導入しました。ノイズモデルを基にエラー緩和法をそれぞれの計算方法に適用しました。その結果、周期駆動系の量子回路における駆動の回数が十分大きい場合、両方法で得られた結果は、それぞれスクランブリング状態に期待される結果と統計誤差[10]の範囲で一致することを確認しました（図1は量子状態の復元に関する計算結果を示しています）。これにより、量子情報の復元や量子多体系計算に役立つと期待される特性を持つスクランブリング状態が、実際に量子コンピュータ上で生成できていることを示しました。

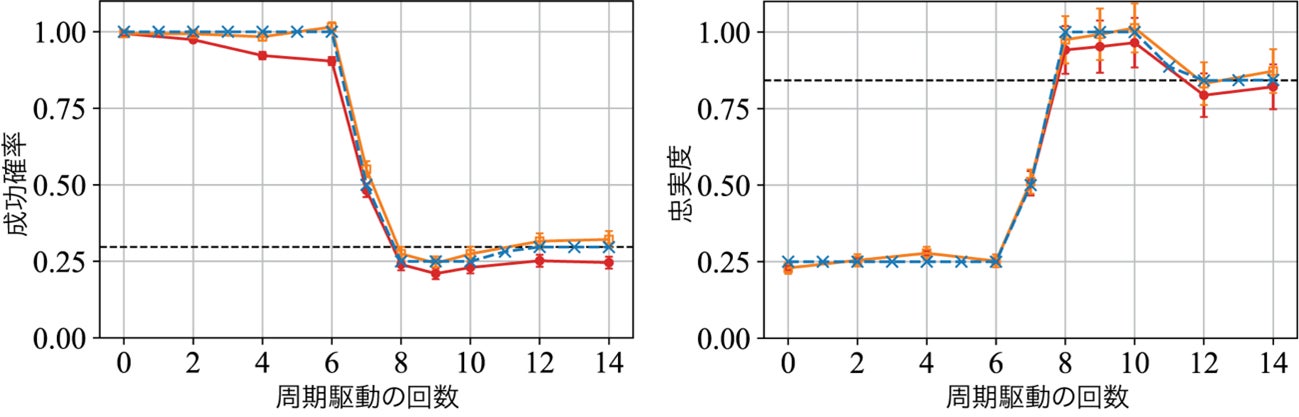
周期駆動系の量子回路に投入した情報を復元する成功確率（左）と復元された状態の忠実度（右）を、周期駆動の回数の関数としてプロットした図。周期駆動の回数は、量子アルゴリズムにおける計算時間の指標である量子回路の深さに比例する。赤い丸のデータはエラー緩和を行っていない結果、オレンジの四角のデータはエラー緩和を行った結果、青いバツ印は誤りのない理想的な場合の結果を示す。黒い破線はスクランブリング状態で期待されるそれぞれの値を示している。周期駆動の回数が大きくなるにつれ、得られた結果がスクランブリング状態で期待される値に近づくことが分かる。

　さらに、スクランブリング状態の応用として、量子多体系における物理量の統計力学[11]計算を行いました（図2）。具体的には、統計力学計算で用いる行列の対角和[12]を求めるためにスクランブリング状態を利用しました。計算する物理量としては異なる二つの量子ビットの測定結果の相関を表す量（2点の相関関数）を用いました。その結果、高い状態密度を持つエネルギー領域で計算した物理量は、誤りがないと仮定した場合に期待される結果と良い一致を示しました。一方で、低い状態密度を持つエネルギー領域で計算した物理量は、期待される結果との差異や統計誤差が大きくなりました。これらの結果は、今回用いた統計力学計算の定式化によって予測された振る舞いと整合しており、状態密度が小さい領域ではより多くの測定が必要だということが示唆されます。

異なる二つの量子ビットの測定結果の相関（2点の相関関数）のエネルギー依存性の計算結果。赤い丸は量子コンピュータ実機から得られた結果、青い線は誤りがない理想的な場合の結果を示す。二つの青い破線の間は状態密度が大きいエネルギー領域を示し、その間にある黒い破線は状態密度が最も大きいエネルギーを示す。青い破線で囲まれた領域では理想的な結果と統計誤差（赤いバー）の範囲で良い一致を示す。一方、状態密度が小さいエネルギー領域では期待される結果との差異が大きい。

今後の期待
　本研究では、現時点で利用可能な量子コンピュータを用い、スクランブリング状態の準備、検証、応用という重要なステップを一貫して実現できることを例示しました。

　本研究で使用した量子ビット数の最大値は20であり、これは従来のコンピュータによる計算の範囲を超えるものではありません。しかし、2025年1月時点では50量子ビットや100量子ビットを超える規模の量子コンピュータが開発され、これらの一部は研究者による利用が始まっています。本研究の成果は、量子コンピュータの学術利用の黎明期にある現在において、物理現象と量子情報の交錯する学術研究領域における量子コンピュータ利用のベンチマークと位置付けることができます。量子コンピュータの性能指標や可用性がさらに向上すると期待される近い将来においても、計算の大規模化や高精度化を目指す際の比較対象として、量子コンピュータの発展に役立つと考えられます。

　本研究で生成したスクランブリング状態は、従来はランダム性を持つ量子回路を用いて議論されることが一般的でした。しかし、今回の研究により、周期駆動系の量子回路を用いてもスクランブリング状態を準備できることが実証されました。この実証において特に有用だったのが、加熱現象を量子情報理論の観点から検討した点です。

　今後も、これまで知られている現象を量子情報理論の視点から再評価することで、新たな視点を得る可能性が期待されます。こうしたアプローチは、量子コンピュータのさらなる発展とその応用分野の拡大に寄与すると考えられます。

論文情報
＜タイトル＞

Simulating Floquet scrambling circuit on trapped-ion quantum computers

＜著者名＞

Kazuhiro Seki, Yuta Kikuchi, Tomoya Hayata, Seiji Yunoki

＜雑誌＞

Phys. Rev. Research

＜DOI＞

10.1103/PhysRevResearch.7.023032

補足説明

[1] 周期駆動系を模した量子回路、ランダム性を持つ量子回路

　時間的に周期的な外部駆動を受ける系。周期駆動系を模した量子回路は、量子ビット群に対して、特　　定の量子力学的な操作を時間的に周期的に、規則正しく行う。一方で、ランダム性を持つ量子回路は、量子ビット群に対して、さまざまな量子力学的な操作を不規則に行う。

[2] イオントラップ型量子コンピュータ

　量子力学に従う物理系として、電磁場に捕捉（トラップ）されたイオンを用いる量子コンピュータ。

[3] 量子多体系

　量子力学に従い相互作用する多数の粒子から成る系。

[4] 量子ビット

　量子情報媒体の最小単位のこと。ビットとは、データの最小単位であり、1ビットは2通りの値（0か1）を表現できる。量子ビットをある状態に準備し測定すると、0か1のどちらかの測定結果が得られるが、一般に一回の測定でどちらの結果が得られるかは分からない。しかし、状態の準備や測定の仕方を変えずにこの試行を繰り返すと、測定結果の相対頻度（例えば全測定回数に対して0の測定結果が得られる回数の割合）は、状態の準備や測定の仕方で定まるある値（確率）に近づく様子が、現時点で利用可能な量子コンピュータを用いて観察できる。量子力学は、量子ビットをはじめとする物理系の状態や、状態の変化や測定を数式で表現することで、この確率を計算するためのルールを与えている。

[5] NISQ

　現在の量子コンピュータはNISQコンピュータまたは単にNISQと呼ばれており、ノイズあり中規模量子コンピュータなどと翻訳される。NISQはnoisy intermediate scale quantumの略。

[6] H1-2

　クオンティニュアム社のイオントラップ型量子コンピュータ「H1-2」は、理化学研究所和光キャンパスに設置され、「黎明（れいめい）」という名称で、2025年2月3日より稼働している注）。本研究における「H1-2」を用いた結果は、「H1-2」が理研に設置される前に実施された。

注）2025年2月12日お知らせ「量子コンピュータ『黎明』が理化学研究所で本格稼働、量子ハイブリッド高性能コンピューティング新時代を切り拓く」
https://www.riken.jp/pr/news/2025/20250212_1/

[7] 量子情報理論
　量子状態で表される情報の伝わり方を数学的に扱い説明する学問体系。

[8] 成功確率と忠実度の計算

　Hayden-Preskill復元プロトコルにおける量子状態の復元の成功確率の計算と成功したときの量子状態の忠実度の計算。量子状態の忠実度とは、生成した量子状態が所望の量子状態にどれだけ近いかを表す指標のこと。

[9] 量子情報の非局在化の指標を計算

　4点の非時間順序相関関数の計算。相関関数とは、ある時刻と場所における物理量と、別の時刻と場所における物理量（既出の時刻や場所や物理量と重複してもよい）の相関を測る量であり、物理量の積を用いて定義される。非時間順序相関関数とは、相関関数を定義する物理量の積の順序が、前の時刻から後の時刻へという通常の時間順序に従わない相関関数のこと。

[10] 統計誤差

　量子計算では一つの物理量を計算するために試行（状態の準備と測定）を繰り返す。一連の試行で状態の準備や測定の仕方は変えないが、得られる測定結果は一般に試行ごとに異なる。本研究では、一連の試行から得られる標本平均の標準偏差で統計誤差を定義した。

[11] 統計力学

　統計力学とは、多数の微視的な粒子から成る系の平均的な性質を導く学問のこと。ここでの平均とは、巨視的な物理量について与えられた条件に整合するように適当に重み付けした、微視的な状態に関する平均である。巨視的な物理量についての条件とは、記述したい平衡状態を指定するための条件であり、例として、エネルギーの範囲を指定する場合や、温度を指定する場合がある。今回は、指定したエネルギーの範囲に応じて適当に重み付けした微視的な状態に関する物理量の平均を計算した。

[12] 行列の対角和

　行列とは、数字や記号を方眼状に並べたもの。特に、縦と横に並べた数字や記号の数が等しい場合、行列の左上から右下に引いた対角線上にある数字や記号の和が定義でき、この和を行列の対角和という。

研究支援
　本研究は、理研TRIPイニシアティブ（RIKEN Quantum）および、科学技術振興機構（JST）共創の場形成支援プログラム「量子ソフトウェアとHPC・シミュレーション技術の共創によるサスティナブルAI研究拠点（研究代表者：藤堂眞治、JPMJPF2221）」、日本学術振興会（JSPS）科学研究費助成事業研究活動スタート支援「ドープされたモット絶縁体における擬ギャップ現象の研究（研究代表者：関和弘、JP19K23433）」、同基盤研究（B）「自己駆動する集団におけるカイラル輸送現象の研究（研究代表者：早田智也、JP21H01007）」「ハミルトニアン形式を用いた非平衡及び高密度QCDの研究（研究分担者：早田智也、JP21H01084）」「ゲージ理論のための量子計算手法の開発と非平衡現象への応用（研究代表者：早田智也、JP24K00630）」、同基盤研究（A）「量子多体系に対する量子-古典ハイブリッド量子計算の新展開（研究代表者：柚木清司、JP21H04446」、同基盤研究（C）「強相関系のための量子計算手法の研究と開発（研究代表者：関和弘、JP22K03520）」による助成を受けて行われました。

　なお、本研究の成果の一部は、NEDO（国立研究開発法人新エネルギー・産業技術総合開発機構）の「ポスト５Ｇ情報通信システム基盤強化研究開発事業（JPNP20017）」の委託事業「計算可能領域の開拓のための量子・スパコン連携プラットフォームの研究開発（研究代表者：佐藤三久）」の結果得られたものです。

発表者・機関窓口
＜発表者＞　※研究内容については発表者にお問い合わせください。

理化学研究所

　量子コンピュータ研究センター　量子計算科学研究チーム

　　研究員　　　　　　　　　関　和弘（セキ・カズヒロ）

　開拓研究所　柚木計算物性物理研究室

　　主任研究員　　　　　　　柚木清司（ユノキ・セイジ）

　　（計算科学研究センター　量子系物質科学研究チーム　チームプリンシパル、量子コンピュータ研究センター　量子計算科学研究チーム　チームディレクター、創発物性科学研究センター　計算量子物性研究チーム　チームディレクター）

Tel: 050-3502-3917（関）

Email: kazuhiro.seki@riken.jp（関）、yunoki@riken.jp（柚木）

クオンティニュアム株式会社

　リードR&Dサイエンティスト　菊池勇太（キクチ・ユウタ）

　（理研　数理創造研究センター　客員研究員）

Email: yuta.kikuchi@quantinuum.com