千葉工業大学・東邦大学・中部大学・高知大学・大阪成蹊大学・大和大学の研究チーム、カオス共鳴により、微弱な信号を捉える次世代センシング技術に応用可能な原理を確立

－従来手法が困難だった「非対称」な系でも高感度検出を実現－

千葉工業大学

2026年1月29日 14時00分

【発表者】

・Anh Tu Tran　（千葉工業大学大学院情報科学研究科（博士後期課程３年））

・信川　創　（千葉工業大学大学院情報科学研究科（教授）/同大学数理工学研究センター（非常勤主席研究員）/国立研究開発法人国立精神・神経医療研究センター精神保健研究所児童・予防精神医学研究部（客員研究員））

・我妻　伸彦（東邦大学理学部情報科学科（准教授））

・稲垣　圭一郎（中部大学理工学部 AIロボティクス学科（教授））

・道法浩孝（高知大学教育学部学校教育教員養成課程（教授））

・山西輝也（大阪成蹊大学データサイエンス部（教授））

・西村　治彦（大和大学情報学部（教授）/兵庫県立大学大学院応用情報科学研究科（名誉教授））

【概　要】

　Tran Anh Tu 博士後期課程学生、信川創教授（千葉工業大学）、我妻伸彦准教授（東邦大学）、稲垣圭一郎教授（中部大学）、道法浩孝教授（高知大学）、山西輝也教授（大阪成蹊大学）、西村治彦教授（大和大学）らの研究チームは、カオス共鳴（Chaotic Resonance）と呼ばれる現象を利用して、極めて微弱な信号を増幅し高感度で捉える際、システムが持つ構造的な「非対称性」が制御の妨げになるという課題を克服する新しい制御手法「Double-Gaussian-Asymmetric-filtered Reducing-Region-of-Orbit (DGA-RRO)法」を開発しました。従来の制御手法（DG-RRO法）は対象システムが対称であることを前提としており、現実の電子回路や生体システムのような非対称性を持つ環境下では、信号検出感度が著しく低下するという問題がありました。今回開発されたDGA-RRO法は、システムの軌道が局所的に滞在するそれぞれの領域に対し、独立した強度のフィードバック制御を適用することでこの問題を解決しました。数値シミュレーションによる検証の結果、DGA-RRO法は従来手法と比較して、非対称な条件下でも高い入出力相関（同期性能）を実現し、より弱いフィードバック強度でカオス共鳴を誘発できることが実証されました。また、実環境を想定した加法性ノイズおよび混入ノイズ（Contaminant noise）が存在する環境下においても、DGA-RRO法は高い堅牢性を示しました。本成果は、神経演算や高感度センシング、省電力通信など、微弱な信号処理が求められる工学分野において、実環境の非対称性に適応可能な新しい基盤技術となることが期待されます。この研究成果は、2026年1月12日に米国の世界最大規模の電気電子工学系学会（IEEE）が発行する学術雑誌IEEE Accessにて発表されました。

キーワード: カオス共鳴、非対称カオスシステム、フィードバック制御、非線形ダイナミクス、同期現象

■研究の背景

1. カオス共鳴とカオス・カオス間欠性（CCI）

　非線形システムにおいて、ノイズや揺らぎが微弱な入力信号への応答（同期）を促進する現象として「確率共鳴（Stochastic Resonance: SR）」が知られています[1]。これと同様に、カオスシステム特有の内的ゆらぎ（カオス的変動）を利用して微弱信号との同期を強める現象を「カオス共鳴（Chaotic Resonance: CR）」(用語説明1)と呼びます。カオス共鳴は、システムが複数のカオスアトラクタ間を行き来する「カオス・カオス間欠性（Chaos-Chaos Intermittency: CCI）」と呼ばれる状態にある時に生じ、確率共鳴よりも高い感度で信号を検出できることが示されています[2]。

2. 従来の制御手法とその課題：RROからDG-RROへ

　カオス共鳴は、メモリデバイスや通信システム、生体医工学などへの応用が期待されていますが、システム内部のパラメータを精密に調整する必要があり、その制御は困難でした。この課題に対し、外部からのフィードバック信号(用語説明2)によって軌道を調整し、強制的にCCI状態（カオス共鳴）を引き起こす「軌道領域減少法（Reduced Region of Orbit: RRO）法」が提案されました[3][4]（右図を参照）。さらに、この手法を改良し、写像の極値付近にのみガウスフィルタ状のフィードバックを与えることで、より低エネルギーかつ高感度な制御を実現する「二重ガウスフィルタRRO（DG-RRO）法」が開発されました[5]。

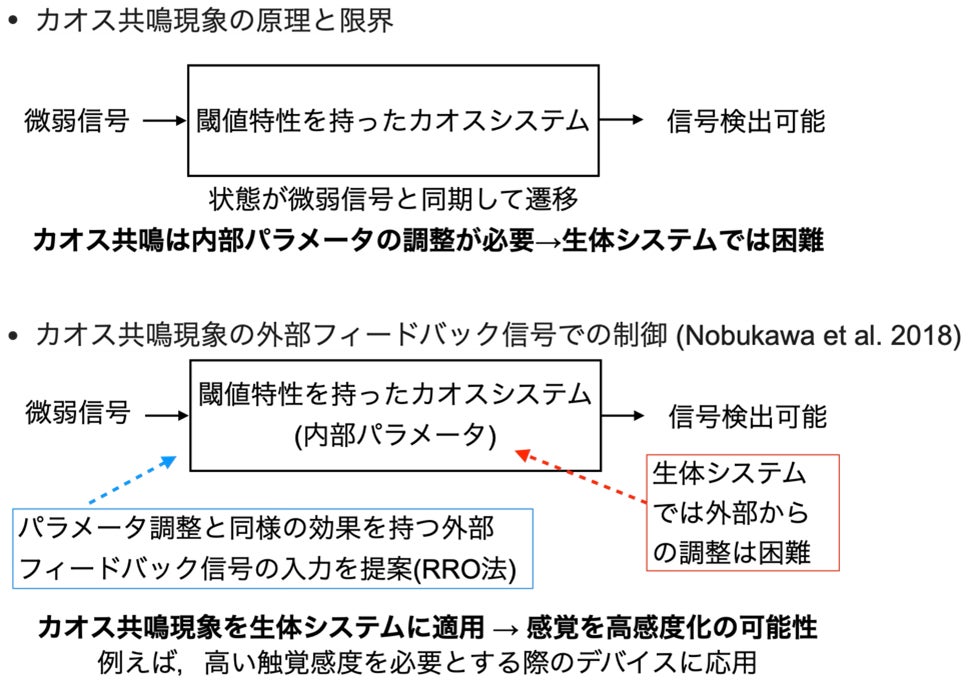
3. 実システムにおける「非対称性」の壁

　これまでのDG-RRO法などの研究は、主に対称的な構造を持つシステムを対象としていました。しかし、現実世界のシステム（電子回路や神経モデルなど）は、構造的な「非対称性」(用語説明3)を持っていることが一般的です。対称性を前提としたDG-RRO法を非対称なシステムに適用すると、以下の問題が生じます。

応答の不均衡: システムの軌道が滞在する各アトラクタ領域に対し、同じ強さのフィードバックを与えても、構造が非対称であるため応答が異なります。

アトラクタ併合の阻害: カオス共鳴に必要な「アトラクタ併合（Attractor Merging）」という現象を左右同時に引き起こすことができず、片側のアトラクタに閉じ込められたり、適切な遷移が起きなかったりします。

効率の低下: その結果、同期性能（信号検出能力）が著しく低下し、制御に必要なフィードバック強度も増大してしまいます。

4. 本研究の動機

　非対称なシステムにおいて高感度なカオス共鳴を実現するためには、システムの歪みに合わせて、アトラクタの左右それぞれの分岐条件を独立して制御できる手法が必要です。本研究では、従来のDG-RRO法を拡張し、左右のガウスフィルタの強度を個別に調整可能にした「非対称二重ガウスフィルタRRO（Double-Gaussian-Asymmetric-filtered RRO: DGA-RRO法）」を提案し、その有効性を検証することを目的としています。

■研究内容

1. 提案手法：DGA-RRO法

　本研究チームは、システムの構造的な非対称性を補正し、カオス共鳴を最大化するための新しいフィードバック制御手法「DGA-RRO」を考案しました（下図）。

・独立したフィードバック制御の導入: 従来の制御手法（DG-RRO法）は、システムの軌道における極大値・極小値付近に対し、同一の強度を持つガウスフィルタを適用するものでした。これは対称なシステムには有効ですが、非対称なシステムでは左右のバランスを崩す原因となっていました。これに対しDGA-RRO法は、システムの軌道が滞在する2つの領域に対し、それぞれ独立して調整可能なフィードバック強度を持つガウスフィルタを配置しました。

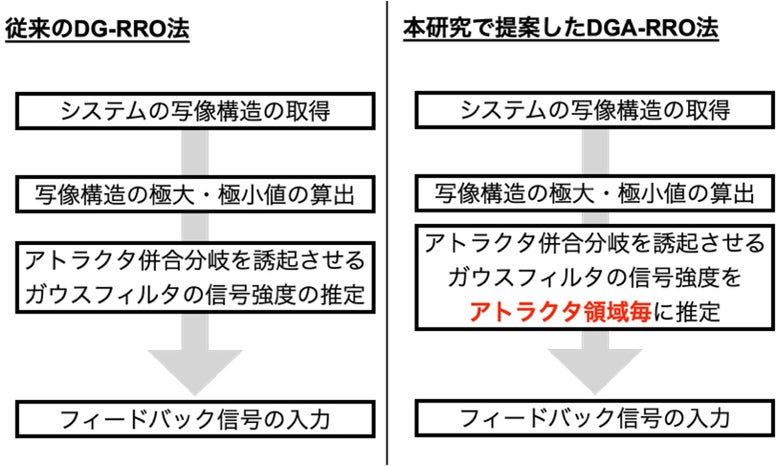
・アトラクタ併合の精密制御: カオス共鳴を高感度で発生させるためには、システムが持つ複数のアトラクタ（安定状態の領域）が結合する「アトラクタ併合（Attractor Merging）」という現象を、入力信号のタイミングに合わせて引き起こす必要があります。DGA-RRO法では、それぞれのアトラクタ領域に対して、フィードバック強度を個別に最適化することで、システムが本来持っている「歪み」に応じて作用します。これにより、非対称な構造を持つシステムであっても、左右両方のアトラクタ併合条件を同時に、かつ精密に満たすことが可能となりました。

2. 数値シミュレーションによる検証と成果

　非対称な3次写像モデルを用いて、様々な条件下での信号検出能力（同期性能）を検証し、以下の優位性を実証しました(右図を参照)。

・非対称環境下での圧倒的な同期性能: システムの非対称度を変化させて検証した結果、従来手法（DG-RRO法）は非対称性が増すにつれて同期性能が急激に低下しました。一方、DGA-RRO法は非対称度が高くなっても、左右のフィードバックバランスを適応させることで、極めて高い同期性能を維持し続けました。

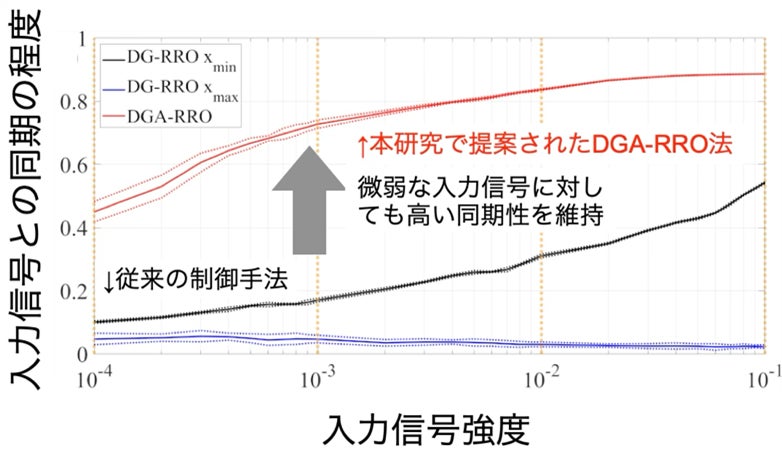
・最小限のエネルギーによる高効率な制御: 制御に必要なフィードバック信号の強さ（摂動の大きさ）を比較したところ、DGA-RRO法は従来手法よりも小さなエネルギーでカオス共鳴を誘起できることが確認されました。これは、システム全体を無理やり制御するのではなく、分岐点付近の局所的なダイナミクスをアトラクタの領域毎に個別に最適化するため、無駄な干渉が生じないためです。

・実環境ノイズに対する堅牢性（ロバストネス）: 現実のシステムには避けられない2種類のノイズ環境下での性能を評価しました。

　➤加法性ノイズ（外部ノイズ）: 信号に混入する一般的なノイズに対して、DGA-RRO法は従来手法よりも広いノイズ強度範囲で高い相関を維持しました。

　➤混入ノイズ（内部パラメータ変動）: システム内部のフィードバックループに混入するノイズ（Contaminant noise）に対して、DGA-RRO法は特に顕著な強さを示しました。従来手法が機能しなくなるような強いノイズレベルであっても、DGA-RRO法は高い同期性能を維持しました。

　以上の結果から、DGA-RRO法は理想的なシミュレーション環境だけでなく、構造的な歪みや予期せぬノイズが存在する現実的な物理・生体システムにおいても、微弱信号検出技術として極めて有効であることが示されました。

■結論と今後の展望

　本研究により、現実世界に不可避な「構造的な歪み」を持つシステムであっても、カオス共鳴を利用して微弱な信号を高感度で検出できることが実証されました。この技術は、神経演算や高感度センシング、省電力制御など、微弱な信号処理が求められる工学分野において、実環境の非対称性に適応可能な新しい基盤技術となります。具体的には、通信システム、パワーエレクトロニクス、脳型情報処理デバイスなど、多岐にわたる分野への応用が期待されます。今後は、より複雑な挙動を示すシステムへの適用や、実ハードウェアへの実装に向けた研究を進めていきます。

■用語説明

1. カオス共鳴: システム内部のカオス的な（不規則な）振る舞いを利用して、外部からの微弱な信号にタイミングを合わせ（同期し）、信号を増幅して検出する現象。

2. フィードバック制御: システムの現在の状態を測定し、その結果に基づいて入力を調整することで、システムを目的の状態に導く制御方法。

3. 非対称性: システムの性質が均一ではなく、偏りや歪みがある状態。現実の物理システムや生物の神経系は、完全な対称ではなく非対称性を持っていることが多い。

■引用文献

[1] Pikovsky, A., M. Rosenblum, and J. Kurths. "Synchronization: A universal concept in nonlinear sciences (Cambridge Univ Pr)." (2003).

[2] Anishchenko, Vadim S., et al. Nonlinear dynamics of chaotic and stochastic systems: tutorial and modern developments. Vol. 111. Berlin: Springer, 2007.

[3] Nobukawa, Sou, et al. "Controlling chaotic resonance in systems with chaos-chaos intermittency using external feedback." IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 101.11 (2018): 1900-1906.

[4] Nobukawa, Sou, et al. "Resonance phenomena controlled by external feedback signals and additive noise in neural systems." Scientific reports 9.1 (2019): 12630.

[5] Iinuma, Takahiro, et al. "Controlling Chaotic Resonance with Extremely Local-Specific Feedback Signals." IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 107.8 (2024): 1106-1114.