茨城高専4年生の共著論文が数学の国際専門誌に掲載

～トポロジーの難問を解くカギとなる結び目データ構造の発見～

　独立行政法人国立高等専門学校機構 茨城工業高等専門学校（茨城県ひたちなか市　校長：米倉達広　以下「茨城高専」） 機械・制御系4年生の山田海音（やまだ・かいと）さんが、同校の伊藤昇（いとう・のぼる）講師との共著論文を執筆し、数学の国際専門誌「JP Journal of Geometry and Topology」に投稿。査読（同分野の研究者に論文の内容を評価してもらうこと）を通過し、6月28日に査読を通過した信頼性の高い論文として採択され、11月1日発行の同誌に掲載された。18歳（採択当時）の高専生が国際専門誌に査読付の論文を発表するという快挙となった。
　結び目理論は、現在活発に研究されている分野で、工業、化学、デザイン等の幅広い分野で応用されている。今回の研究はDNA解析や材料研究といった分野での発展が期待される。

茨城高専4年生の山田海音さん（写真：左）と同校の伊藤昇講師（写真：右）

■論文内容
山田さんが発見したのはトポロジー（位相幾何学）（注1）の１つである結び目理論（注2）の難問を解くカギとなるデータ構造。共著者の伊藤講師は2020年、結び目理論の中で60年以上続いていた「結び目を境界とする曲面の形の決定問題」の解決につながる画期的な論文（※1）を発表し、世界的な反響を呼んだ。山田さんと伊藤講師の研究は、コンピューターを使って伊藤講師の前掲論文が説明した「結び目膜と結び目膜の間の変形」を実際に描き出す効率的な方法を導き出した。
 

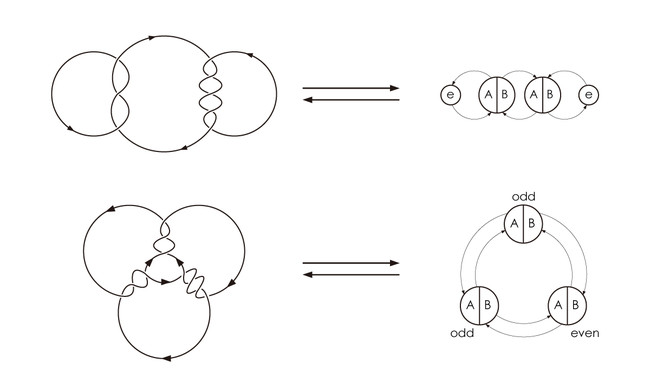複雑な結び目を簡易化する山田海音の計算方法

■研究分担
今回の研究で山田さんは、曲面を効率的に描写する上でポイントとなるねじられた帯（注3）について、従来とは全く異なる方法で捉えるデータ構造を理論的に編み出した。伊藤講師は曲面同士に発生する演算を理論的に拡張させることで、この山田さんの理論を裏付けた。

 ■研究の意義
２人の見出したこの理論を用いると、簡単な曲面から複雑な曲面へとメビウスの帯数が増える結び目の絵を短時間で出力することにつながる。これは現在の世界最先端の水準を大きく上回るプログラム計算となりうるもので、現在、山田さんはその実装に向けた研究を進めている。

■今後の展望
本校入学後、ハッカソンやロボコンなどで技術や知識を身につけてきた山田さん。今回の快挙について「最初に伊藤先生から結び目理論についてお話を伺ったときに、『これはグラフ（注4）だな』と思い、日本語で草案を書きました。それを伊藤先生が英訳と数学方面からの裏付けをしてくださり、論文という形で発表することができました。伊藤先生と奥出先生（同校 情報系教授）にチェックしていただきながら厳密性と簡潔さを意識して書くことができたので、それが評価されたようで嬉しいです」と述べ、今後については 「結び目に対する本質的な理解が浅いまま書いてしまいましたが、その分柔軟で新規性のあるデータ構造になっています。この先は数学的な方向からの厳密性を追いつつ、実装を進めていきたいと思います」と意気込みを熱く語った

■参考
論文情報
雑誌名：「JP Journal of Geometry and Topology」
論文タイトル：Plumbing and computation of crosscap number
著者：Noboru Ito, Kaito Yamada
URL：http://www.pphmj.com/journals/jpgt.htm

（※1）伊藤講師が2020年に発表した論文情報はこちら
雑誌名：「International Journal of Mathematics」
論文タイトル：Crosscap number of knots and volume bounds
著者：N. Ito, Y. Takimura
URL：https://www.worldscientific.com/doi/epdf/10.1142/S0129167X20501116
 
＜要旨＞
この論文では、伝統的に知られている曲面の演算の変形版を与えた。論文ではまた、クロスキャップ数（注5）をカウントするコンピューター計算にフィットしたデータ構造を導入した。
 
＜本研究の発展性に関して＞
山田海音さんのプログラムをチェックした奥出真理子教授のコメント
『伊藤先生の理論をシンプルなネットワークモデルに変換し、山田さんのオリジナルアイデアでコンピューター計算できるモデルを作った点が良かった。今後は構造解析の分野や、複雑ネットワークを解いていく上で応用を期待したい。』
 

• ＜用語解説＞
• （注1）トポロジー（位相幾何学）：何らかの形を連続変形しても保たれる図形的性質を研究する幾何学（図形や空間の性質について研究する数学の分野）。
• （注2）結び目理論：紐の結び目を数学的に表現し研究する学問。
• （注3）ねじられた帯（メビウスの帯）：細長い帯を1回ねじって両端をはり合わせたときに、表裏の区別ができない連続面となる図形。
• （注4）グラフ：点と辺からなる図形のことでトポロジーの研究対象のひとつ。
• （注5）クロスキャップ数：曲面に含まれるメビウスの帯数。

茨城工業高等専門学校について
茨城工業高等専門学校は、国境を意識させない２１世紀型グローバルスタンダードの教育内容と教育環境を内外の若者に提供します。また学生の知的好奇心の段階的成長を手助けし、科学技術や工学の社会との関わりを教授して、起業家精神を身につけることにより両者を結び付け、社会の成り立ちを理解できる基盤を育成します。職業選択だけでなく人生設計と自立する技術者としてたくましく生きるための準備はグローバルキャリヤ教育として実施します。これらを従来の専門技術教育に加味して、次世代を担うたくましい技術者人材を育成します。

【学校概要】
学校名：独立行政法人国立高等専門学校機構　茨城工業高等専門学校
所在地：茨城県ひたちなか市中根866
校長名：米倉　達広
設立：１９６４年
URL：https://www.ibaraki-ct.ac.jp/
事業内容：高等専門学校・高等教育機関

【本リリースに関する報道お問い合わせ先】
茨城工業高等専門学校　広報室　金澤／酒向
TEL：[phone]
E-mail：[e-mail]